Interferencia

Condiciones para la interferencia

Cada onda de luz sigue su propia senda independiente de la de todas las demás, de modo que si se superponen dos ondas en un mismo medio, el efecto oscilatorio resultante en las partículas del mismo –desde su posición media en cualquier instante– es el resultante de dos desplazamientos individuales. Ese desplazamiento resultante (Y) en la dirección y de la ecuación
φ = (α / r) sen (ωt – Kr)
puede tener la forma
Y = A sen (ωt – θ)
donde A es la amplitud y θ la fase.
Si las ondas originales fueron coherentes, por ejemplo, de idéntica longitud, amplitud (α)y diferencia de fase constante(δ), entonces pueden producirse efectos de interferencia. La intensidad resultante nos la da
I ≈ A2 = 4α2 cos2 (δ / 2)
Si es 0, 2π, 4π ,,, entonces I tiene una intensidad de cuatro veces la de cualquiera de los haces, a la que se denomina interferencia constructiva. Pero si I es π, 3π, 5π…, entonces la intensidad es cero y se denomina interferencia destructiva. Estos efectos de interferencia pueden tener valores intermedios. La interferencia también se produce donde las ondas son de diferentes amplitudes, pero las longitudes de onda deben ser idénticas y la diferencia de fase fija.
Produciendo interferencia

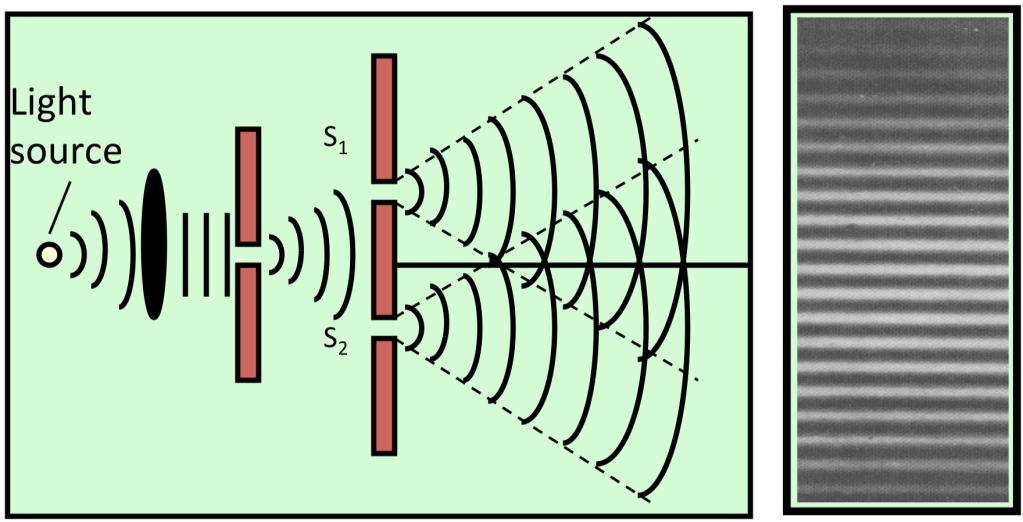
Para asegurar la coherencia de los dos haces, si no provienen de una fuente láser, se originan a partir de la misma fuente de una de las siguientes dos maneras. La primera es la división de frente de onda por medio de un arreglo físico, tal como los cortes estrechos en una rejilla de difracción, cuando los frentes de onda coherentes emergentes adyacentes interfieren para ofrecer un patrón de bandas oscuras y claras llamado bordes de interferencia.
La segunda es por división de amplitud, donde el frente de onda se divide en dos frentes de onda menos intensos mediante un dispositivo como una película delgada, que introduce una diferencia de fase entre los componentes reflejados frontales y traseros, causando una discrepancia en las sendas ópticas debido a su anchura (t).
Esto conduce a la condición, para una película de índice de refracción n, de que –para la interferencia– la discrepancia en la senda debe ajustarse a
2nt cos r = kλ
donde λ es el orden de interferencia. En concreto, cuando λ = 0, 1, 2…se produce interferencia destructiva y cuando λ = 1/2, 3/2, 5/2… se produce interferencia constructiva.
Esta relación se aplica en revestimientos de película fina sobre materiales ópticos para reducir o incrementar la reflexión.
Anillos de Newton

Una película fina de aire, como la que hay entre una lente convexa y la superficie de un plano, proporciona una serie concéntrica de bordes oscuros y claros –que se denominan anillos de Newton– cuya utilidad es clave para determinar la topografía de la superficie de una lente durante su fabricación. Para una superficie con radio de curvatura R y un borde de radio r, la anchura de la película de aire t nos la da
t = r2 / 2R
La luz monocromática proporciona un patrón de borde concéntrico extenso.
Otros sistemas que contienen una película de aire, como los que se encuentran entre la base de un negativo o positivo fotográfico y una placa de presión o una diapositiva velada, exhiben patrones irregulares a los que también se denomina (de manera incorrecta) anillos de Newton.
4. Visibilidad de los bordes
La claridad del patrón de borde se puede cuantificar en términos de su visibilidad (V) que se define como
V = (Imax – Imin) / (Imax + Imin)
Esta formula tiene aplicaciones importantes relacionadas con la medición del contraste de la imagen.
Difracción
Difracción de Fraunhofer
Cuando un haz de luz pasa a través de una apertura estrecha, se dispersa en una pequeña cantidad hasta la región de la sombra geométrica. Este ejemplo sencillo de difracción es un ejemplo de luz que no consigue viajar en línea recta, pero se puede explicar considerando el borde de la apertura como una fuente de ondículas secundarias.
Como los haces principal y secundario son coherentes, se puede producir interferencia y se puede observar un patrón de bordes de difracción. Cuando la fuente de iluminación y el patrón se encuentran distantes de la apertura, se observa difracción de campo lejano o difracción de Fraunhofer, que no cambia de forma con la distancia. La difracción de Fresnel tiene una fuente y un patrón cercanos que cambian con la distancia.
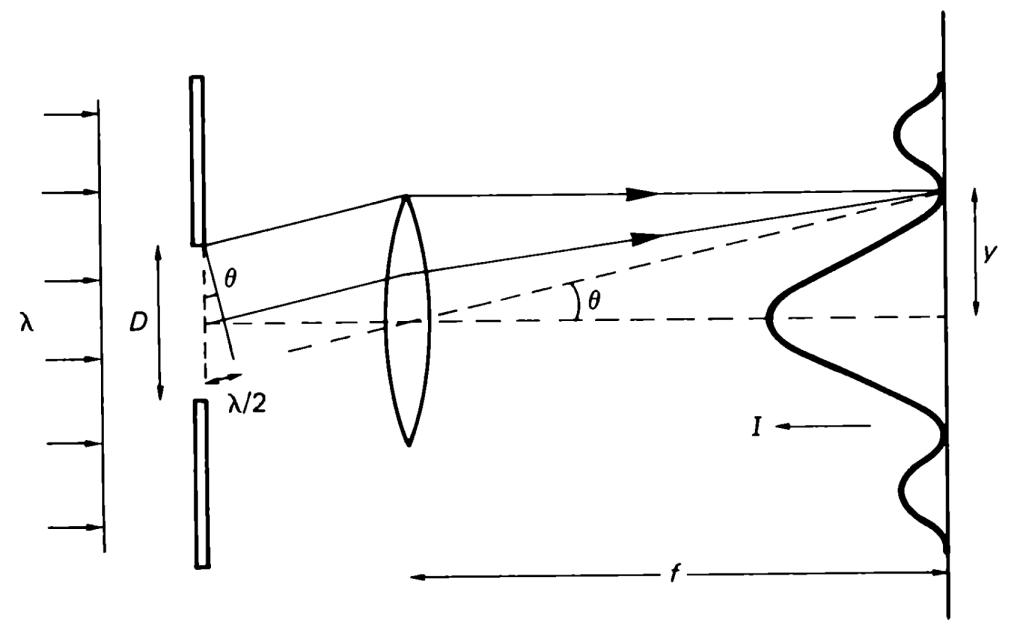
Analizar un tratamiento completo de difracción va más allá de los propósitos de este artículo, pero el tratamiento simplificado de ciertos comportamientos de difracción resulta útil a la hora de considerar el poder de resolución de los sistemas ópticos. Tomemos, por ejemplo, la difracción de Fraunhofer en un corte simple de anchura D en la onda de plano monocromática λ, donde el patrón se reproduce por medio de una óptica de longitud focal f, para el primer borde oscuro y donde la Diferencia entre Sendas Ópticas (OPD, por su acrónimo en inglés) entre la iluminación periférica y el borde es λ/2:
sen θ = λ/2
y
tan θ = y/f
Para ángulos pequeños, sen θ = tan θ = θ, así que
y = f θ = mfλ / D
La posición de otros bordes oscuros la proporcionan múltiplos enteros de esta ecuación, de manera que la distancia del tercer borde oscuro con respecto al eje óptico es 3fλ / D, ya que m = 3.
Si se reemplaza el corte por una apertura circular, como sería el caso en la mayoría de las ópticas cinematográficas, el patrón de difracción cambia a uno de luz concéntrica y anillos oscuros alrededor de un punto central brillante. Para una óptica cuyo rendimiento sólo esté limitado por la difracción, que se denomina limitada por difracción, esta distribución de la intensidad constituye el patrón de Airy, o también la Función de Dispersión del Punto(PSF, por su acrónimo en inglés) de la óptica. La zona central del primer “anillo oscuro” se suele llamar “el disco de Airy”.

Sustituyendo y en la ecuación tan θ = y/f por r, el radio del primer anillo oscuro, una derivación difícil muestra que el valor de m ya no es entero y toma los valores 1.22, 2.233, 3.238, 4.241 etc. De ahí que para r
r = 1,22λf / D
El valor de f / D es obviamente la apertura relativa de la óptica, denominada N:
r = 1,22λN
La ecuación y = f θ = mfλ / D muestra que los efectos de la difracción se incrementan cuando D se reduce y cuando λ aumenta.
La rejilla de difracción
La difracción se emplea en forma de una rejilla de cortes situados muy próximos entre sí, con un espaciado de centro a centro de d. y la luz incidente policromática se difracta según la longitud de onda, como se especifica en la ecuación d (sen i + sen θ) = mλ. De especial utilidad resulta el diseño de la rejilla de transmisión trazada que se suele hacer por medio de un proceso de replicado, en el cual se forman surcos en prismas diminutos cuyo ángulo de difracción iguala al ángulo de difracción θ. Los surcos pueden ser de 2-30 μm de ancho y el ángulo de trazado de 1-30º.
La placa de zona

Es una forma especial de rejilla de difracción, que consiste en zonas concéntricas alternativas oscuras y claras, cuyos radios son proporcionales a las raíces cuadradas de números enteros. Por la difracción de Fresnel y el bloqueo de ciertas amplitudes, el patrón de difracción es un punto central intenso. Como las zonas de transmisión pasan sólo rayos que son múltiplos enteros de una longitud de onda desfasada y –por lo tanto– constituyen una interferencia constructiva, la variación de difracción con zona concentra los rayos en un punto. La placa de zona se comporta de manera muy similar a la de una lente simple, con la distancia de la fuente y la distancia del punto de imagen obedeciendo la ecuación conjugada de las lentes. La longitud focal de la placa de zona se da como:
f = S12 / λ
donde S1 es el radio de la primera zona.
En los próximos artículos trataremos sobre el filtrado espacial y la polarización.
